Feathering a mask for anti-aliased sprites
Cartoons are often shot at 12 frames per second (fps), yet the animation looks remarkably fluid. Japanese cartoons sometimes go as low as only 8 frames per second. Animation on a computer requires a much faster refresh rate to convey fluency, however; 20 to 30 frames per second are not uncommon. This difference can be partially explained by "motion blur". Cartoon animators use motion blur to suggest motion even in still images. Sprites, on the other hand are drawn with sharp edges and "unblurred". In computer animation, motion blur is often too costly to do in real-time. Animation with sprites that have smoothed edges is a compromise: it makes the animation look smoother at a lower refresh rate and it is less expensive (in CPU cycles) than motion blur.
Image composition with an alpha channel copies a foreground image (or a sprite) into a background image under the control of a mask. For every pixel in the sprite, the mask has a value that gives the translucency value of that sprite pixel.
The mask value ranges from transparent to opaque. In standard sprite engines, the mask is a "bit mask", and it can only give these two values for every sprite pixel: transparent or opaque. Alpha channel masks often use 8 bits to give a percentage of the transparency of the sprite pixel. Usually, 0 means opaque and 255 means transparent. When the mask value is 192, for example, the pixel is 75% transparent, or 25% opaque.
In this article, I will refer to alpha blending when a mask supports semi-transparent pixels. That is, it should have more than 1 bit for every mask value. I furthermore assume that an alpha mask has 8 bits per mask value. This is the most common format of an alpha mask.
The advantage of a bi-level (which supports only fully transparent and fully opaque) is that you can easily create a mask from a sprite image by designating one colour of the sprite as "transparent". This is known as "chroma keying".
One common use for alpha blending is to avoid the "jaggies" when blitting a sprite in the background image. You basically make a bi-level mask, and then soften the edges of the mask (called "feathering" a mask). This article proposes two algorithms for that purpose.
The feathering of the mask edges looks similar to "blurring", but there is an important difference: you should only blur the non-transparent areas of the mask. The transparent areas of the mask should not be blurred, because the pixel values of sprite image are undefined (usually black) at the locations where the sprite should be transparent.
The first algorithm uses a simple filter matrix that runs over the mask.
| 0 1 0 |
1/5 | 1 1 1 |
| 0 1 0 |
With the restriction that only opaque pixels run through this filter. In C code, this would lead to:
int smooth_mpixel(int x, int y)
{
int sum;
sum = get_mpixel(source>, x, y);
if (sum == 255) {
return sum; // pixel is transparent, do not filter
} else {
sum += get_mpixel(source>, x - 1, y);
sum += get_mpixel(source>, x + 1, y);
sum += get_mpixel(source>, x, y - 1);
sum += get_mpixel(source>, x, y + 1);
return sum / 5;
}
}
void simple_smooth(int width, int height)
{
int x, y;
for (y = 1; y < height - 1; y++)
for (x = 1; x < width - 1; x++)
set_mpixel(target, x, y, smooth_mpixel(x, y) );
}Here, an "mpixel" is the mask value (or alpha value) at the pixel location (x, y). The function get_mpixel() reads a pixel value from the source image, the function set_mpixel() writes a pixel into the target image. The algorithm needs two images, as to avoid that get_mpixel() reads pixel values that were modified in earlier iterations.
This routine has an asymmetry, which can be both an advantage or a disadvantage: diagonal edges are blurred more than horizontal or vertical edges. To show why, I have put the filter matrix in the following figure on a horizontal edge, a vertical edge and an edge at 45 degrees. Assume that in this figure, a white pixel has value one (1.0) and a gray pixel has value zero (0.0).
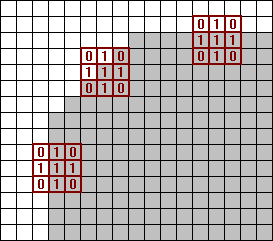
You will see is that the result of the filter matrix is 0.20 when applied to a horizontal or a vertical edge (only 1 white pixel among the five pixels accounted for in the matrix). For a diagonal edge, the result is 0.40 (two white pixels).
The reason that I say that the asymmetry may be an advantage is because only diagonal edges look "jagged". Horizontal and vertical lines do not require much smoothing. Therefore, this algorithm is a compromise that removes the jaggies and keeps much of the sharpness (of the edges).
This compromise is a double edged sword. Its advantage is also its disadvantage. The sharpness of the horizontal and vertical edges draws the attention to the relative fuzziness of the diagonal edges. Sharp corners are smoothed more strongly too and they may appear rounded. This is often undesirable: it makes the sprite look uneven. In addition, if you use the smoothing function to soften the edges of a cast shadow or drop shadow (that you created run time from an object), the asymmetric effect on horizontal/vertical versus diagonal edges and the rounded corners gives unrealistic results.
I have been criticized for that last remark, especially regarding corners of objects. Checking the truth in this matter is as simple as holding an object in the sun and looking at the shadow that this object casts.
Criticism does not bother me, but I urge everyone to think of, and do, experiments to settle an argument.
By choosing different coefficients in the matrix, you can reduce the asymmetry. However, you will always keep special cases (e.g. at corners or angles in the object) with a filter matrix.
Therefore, I will now present an alternative algorithm. This algorithm is based on a technique called "snowing". Snowing is used to create an outline from filled graphic objects, for example as the first step in tracing a bitmap image to a vector drawing. The trick in using snowing to smooth a mask is that you move the outline inwards.
int snow_mpixel(int x, int y, int cur_level, int step)
{
int mvalue = get_mpixel(source, x, y);
if (mvalue < cur_level) {
cur_level -= step;
set_mpixel(source, x, y, cur_level);
} else {
cur_level = 255; /* reset to transparent */
} /* if */
return cur_level;
}
void snow_smooth(int width, int height, int level)
{
int x, y;
int cur_level, step;
int i;
/* To make the feather border level pixels wide, step
* from 255 to 0 in "level" steps. But guard against
* division by zero.
*/
step = level == 0 ? 256 : 256 / level;
/* The two horizontal passes */
for (y = 0; y < height; y++) {
/* snow left */
cur_level = 255; /* assume transparent */
for (x = 0; x < width; x++)
cur_level = snow_mpixel(x, y, cur_level, step);
/* snow right */
cur_level = 255;
for (x = width - 1; x >= 0; x--)
cur_level = snow_mpixel(x, y, cur_level, step);
} /* for */
/* The two vertical passes */
for (x = 0; x < width; x++) {
/* snow top */
cur_level = 255;
for (y = 0; y < height; y++)
cur_level = snow_mpixel(x, y, cur_level, step);
/* snow bottom */
cur_level = 255;
for (y = height - 1; y >= 0; y--)
cur_level = snow_mpixel(x, y, cur_level, step);
} /* for */
}The new routine creates a feathered border that has an equal thickness in all directions.
One essential difference between the "filter matrix" and "snowing" algorithms should not go unmentioned: the snowing algorithm changes a mask in-place; it does not need separate source and target images.
Closing words
Both algorithms use a linear weight scale from opaque to transparent. Both can be extended to non-linear (gamma-corrected) scale. Also, a range of 256 opaqueness levels may be overkill in many situations (like animation). Having fewer steps may drastically reduce the memory footprint and may improve the blitting speed.
How does a filter matrix work?
A filter matrix is a two-dimensional array that contains "coefficients" or weighting levels. When the filter runs over an image, it changes the colour (or the value) of each pixel based on:
- the current value of the pixel and the values of neighbouring pixels
- the coefficients in the filter matrix
The centre of the filter matrix maps to the target pixel. The coefficients around the centre of the matrix map to the pixels around the target pixel in a straightforward manner. Each pixel is multiplied with the coefficient in the filter matrix, and then these products are added together. This summation, possibly multiplied by a global weight factor, is the new value for the target pixel.
A filter matrix, as used here, is sometimes referred to as a convolution filter. The convolution theorem lays a relation between filtering in the frequency domain and filtering in the spatial domain. These theoretical groundings are well beyond the scope of this article —see a book on signal processing for details of this topic.

